| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- disposableeffect
- filternotnull()
- 문자열
- 자바
- 프로그래머스
- 자료형
- Java
- jetpack
- 오블완
- composelifecycle
- 백준파이썬
- 티스토리챌린지
- 자바set
- 자바리스트정렬
- list
- compose
- android
- Provider
- nullpointerexception방지
- Dependency
- 파이썬문법
- ContentProvider
- 파이썬
- Kotlin
- Python
- programmers
- 리스트
- 백준
- 배열
- Hilt
Archives
- Today
- Total
study gomi
Python 거듭 제곱 시간 복잡도 본문
728x90
반응형
Python 거듭제곱 계산 방법
거듭제곱 계산 과정에서 분할 정복 알고리즘을 사용
=> 파이썬에서 거듭제곱 연산 수행할 때는 일반적으로 O(log n)의 시간 복잡도
기본 : ** 연산자/pow함수
- 대부분 문제 없음
- 큰 숫자(ex. a와 b가 모두 큰 수일 경우) => 시간 초과 발생 가능
- gpt 설명 참고 ↓
더보기

이거 시간 복잡도 O(n)으로 알고 있었는데 gpt3.5 말이 몇 번을 물어도 O(log N)이라고 한다.

거듭 제곱 하고 특정 숫자로 나눈 나머지 값까지 한 번에 구하는 방법
(큰 수의 거듭제곱을 다루거나 모듈러 연산이 필요한 알고리즘 문제에서 사용)
- pow(a, b, mod)함수
- 함수 원형 참고 ↓
더보기
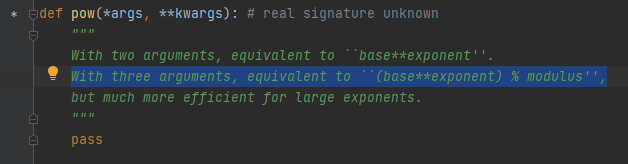

지수 값이 클 때 더 효율적이라고 한다.


- 지수가 큰 경우 사용할 때 효과적
- 효율적인 이유 참고↓
더보기
- 효율적인 거듭제곱 계산: pow 함수는 분할 정복 방식을 사용하여 거듭제곱을 계산합니다. 이 방식은 일반적인 반복적인 곱셈보다 훨씬 빠른 O(log n) 시간 복잡도를 가집니다.
- 모듈러 연산의 통합: pow(a, b, mod)는 a의 b제곱을 계산하면서 동시에 모듈러 연산을 수행합니다. 이는 두 연산을 분리해서 수행하는 것보다 효율적이며, 특히 결과값이 매우 클 때 유용합니다. 결과값이 매우 크면 일반적인 계산 방식으로는 메모리 오버플로우나 시간 초과의 문제가 발생할 수 있습니다.
- 메모리 및 연산 최적화: pow(a, b, mod)는 중간 계산 결과를 mod로 나눔으로써 결과값의 크기를 작게 유지합니다. 이는 메모리 사용을 줄이고, 전체 계산 속도를 빠르게 합니다.
728x90
반응형
'basic > python' 카테고리의 다른 글
| Python list(리스트) 뒤집기 / 거꾸로 / 요소 반대로 역순 출력하기 (0) | 2024.05.14 |
|---|---|
| Python 팩토리얼 함수 - 재귀 (0) | 2024.01.17 |
| Python 덱(deque)의 rotate 메소드 (0) | 2024.01.16 |
| Python 입력 받기 심화 (개수 모를 때 / 특정 문자까지 입력 받기 등) (0) | 2024.01.14 |
| [Python|파이썬] 기본 문법 - 패키지(Package) (0) | 2024.01.14 |
