| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- 백준파이썬
- 자바
- 배열
- ContentProvider
- Kotlin
- 파이썬
- 자료형
- 문자열
- disposableeffect
- android
- Dependency
- 자바set
- jetpack
- Python
- 자바리스트정렬
- Hilt
- compose
- 프로그래머스
- 오블완
- 리스트
- list
- nullpointerexception방지
- filternotnull()
- 파이썬문법
- 티스토리챌린지
- Provider
- Java
- 백준
- composelifecycle
- programmers
- Today
- Total
study gomi
[백준/baekjoon] 4134번 다음 소수 (파이썬/자세한 풀이) 본문
내 제출
- 물론 '단계별로 풀기'를 통해 쉬운 것부터 풀고 있긴 하지만... 근래 풀었던 것 중 가장 어려웠다.
- 이전에 비슷하게 공약수 찾아서 푸는 문제에서 시간 초과가 떴었어서..
- 어떻게 해야 빠르게 답을 찾아내지...? 가 고민이었음.
- 약수, 배수와 소수2 단계에서 이거랑 이전 문제(나무 심는 거였나...?)가 제일 어려운 것 같다.
- 물론 코드 작성에 아주 복잡한 알고리즘 등이 필요한 건 아니었는데 접근이 어려운(?!)
def is_prime(check_n):
if check_n <= 1:
return False
if check_n <= 3:
return True
if check_n % 2 == 0 or check_n % 3 == 0:
return False
i = 5
while i * i <= check_n:
if check_n % i == 0 or check_n % (i + 2) == 0:
return False
i += 6
return True
def find_next_prime(check_n):
while True:
if is_prime(check_n):
return check_n
check_n += 1
# 입력 받기
t = int(input())
for _ in range(t):
n = int(input())
print(find_next_prime(n))
문제 접근
(아주 전문가는 아니라서 틀릴 수도...)
- 소수? 1과 자신 외에는 어떤 수로도 나누어 떨어지지 않는 수
- 소수 판별? 2부터 그 수의 제곱근까지의 모든 수로 나누어 보는 것 => 근데 이렇게 접근하면 시간 초과가 날 것 같았다.
- 문제의 제약 조건이 정수 n(0 ≤ n ≤ 4*10^9) ... 이전에 이것보다 작은 숫자였을 때도 시간 초과가 떴었음.
- 에라토스테네스의 체...? 메모리 제한에 안 걸리려나??
- 사실 이전에 같은 유형의 문제들을 다 맞춰왔다면 고민 안 했을 텐데 전적이 있음...^;;^
- 그래서 4*10^9와 같이 큰 수를 에라토스테네스의 체로 접근하는 건 메모리 제한 때문에 적합하지 않다고 판단.
- 그렇다면 가장 효율적인 방법...? 찾아보니 '밀러-라빈 소수 판별법'이라는 게 있다.
https://goodbyefin.tistory.com/47
밀러 - 라빈 소수 판별법 (Miller - Rabin primality test)
컴퓨터 공학에 입문한 뒤 대부분 처음으로 배우는 소수 판별 알고리즘은 에라토스테네스의 체 알고리즘이다. 에라토스테네스의 체는 소수를 판별하고 싶은 범위 안의 소수인 수의 모든 배수를
goodbyefin.tistory.com
- 이건... 어렵다. 매우 큰 수에 대한 소수 판별에 매우매우 효율적이라는 것은 알겠다.
- 하지만... pass. 나보다 실력이 좋은 사람은 이걸 한번 구현해보는 것이 어떨까?
- 어쨌든... for문만 사용하지 않으면 될 것 같았다.
- 나는 그냥 아주 단순한 태초의 방법을 사용하기로 했다.
- 다행히 정답이었다.
문제 풀이 (코드 풀이)

- 주어진 숫자 n부터 시작하여 n보다 크거나 같은 가장 작은 소수를 찾을 때까지 계속 숫자를 증가시키면서 소수인지 판별.

- 소수 판별에는 2,3으로 나누어 떨어지는지 먼저 확인
- 그 다음에는 5부터 시작하여 6n±1 형태의 수들로만 나누어 보는 방법을 사용
- 위의 경우들로 나누어 진다면 소수가 아님.
- 2,3,5는 왜 체크하는 지 굳이 설명이 필요 없을 것 같고 6n±1의 경우만 설명해보겠음(해당 부분 코드도.)
먼저 6n, 6n±2, 6n±3, 6n±4 형태의 숫자들이 왜 소수가 아닐 수밖에 없는지??
- 6n 형태: 이 숫자들은 분명히 6의 배수이므로 소수가 아님.
- 6n±2 형태: 이 숫자들은 2의 배수 (예를 들어, 6×1+2=8, 6×2+2=14 등).
- 6n±3 형태: 이 숫자들은 3의 배수 (예를 들어, 6×1+3=9, 6×2+3=15 등).
- 6n±4 형태: 이 숫자들도 2의 배수 (예를 들어, 6×1+4=10, 6×2+4=16 등).
그래서 남는 형태는 6n±1!
사실 잘 생각해보면 학창 시절 언젠가... 배웠던 것들이지만..ㅎ
수 교육과정은 대학교 진학하면서 잊어버리는 것 아니겠나요옹? ㅋㅋ
여튼 그래서 이런↓ 반복문을 작성하게 되었다.
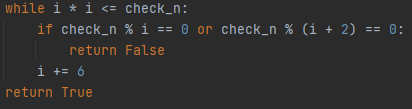
- i는 5부터 시작 (i = 5로 초기화되었음).
- while i * i <= n: 반복문은 n의 제곱근까지만 검사(소수 판별에 필요한 최대 범위.)
- if n % i == 0 or n % (i + 2) == 0: 이 조건문은 두 가지 경우를 검사:
- n % i == 0: 이는 6n - 1 형태의 숫자들을 검사(여기서 i는 5, 11, 17, 23 등.)
- n % (i + 2) == 0: 이는 6n + 1 형태의 숫자들을 검사합니다(여기서 i + 2는 7, 13, 19, 25 등.)
- i += 6: 이 부분은 i를 6씩 증가시켜 다음 6n - 1 형태의 숫자로 이동.
- return True: 만약 n이 이 조건들에 의해 나누어 떨어지지 않으면, n은 소수로 간주.
- 아무튼 이런 ↑ 이유로 6n±1에 대해서만 검사를 한다. 이 숫자들만 소수일 가능성이 있다.
- 물론 모든 6n±1이 소수라는 건 아니지만... 밀러-라빈도 먹히듯이 이것도 먹힐 것이라고 생각해서 작성했다..
결과

https://www.acmicpc.net/problem/4134
'Practice > Baekjoon' 카테고리의 다른 글
| [백준/baekjoon] 13909번 창문 닫기 (파이썬) (1) | 2024.01.11 |
|---|---|
| [백준/baekjoon] 17103번 골드바흐 파티션 (파이썬) (1) | 2024.01.11 |
| [백준/baekjoon] 2485번 가로수 (파이썬) (1) | 2024.01.10 |
| [백준/baekjoon] 1735번 분수 합 (파이썬) (0) | 2024.01.09 |
| [백준/baekjoon] 2798번 블랙잭 (파이썬, c++) (0) | 2024.01.05 |




